Boosting Randomized Smoothing with Variance Reduced Classifiers
Mark Niklas Müller, Marc Fischer
April 15, 2022
Deep neural networks often achieve excellent accuracy on data $x$ from the distribution they were trained on. However, they have been shown to be very sensitive to slightly perturbed inputs $x+ \delta$, called adversarial examples. This severely limits their applicability to safety-critical domains. Further, heuristic defenses against this vulnerability have been shown to be breakable, highlighting the need for provable robustness guarantees.
A promising method providing such guarantees for large networks is Randomized Smoothing (RS). The core idea is to obtain probabilistic robustness guarantees with arbitrarily high confidence by adding noise to the input of a base classifier and computing the majority vote of the classification over a large number of perturbed inputs using Monte Carlo sampling.
In this blogpost, we consider applying RS to ensembles as base classifiers and explain why they are a particularly suitable choice. For this, we will first give a short recap on Randomized Smoothing, before explaining our approach and discussing our theoretical results. Finally, we show that our approach yields a new state-of-the-art in most settings, often even while using less compute than current methods.
Background: Randomized Smoothing (RS)
We consider a (soft) base classifier $f \colon \mathbb{R}^d \mapsto \mathbb{R}^{n}$ predicting a numerical score for each class and let \(F(x) := \text{arg max}_{i} \, f_{i}(x)\) denote the corresponding hard classifier $\mathbb{R}^d \mapsto [1, \dots, n]$. Randomized Smoothing (RS) takes such a base classifier, evaluates it on a large number of slightly perturbed versions of an input, and then predicts the majority classification over the resulting predictions. The bigger the difference between the probability of the most likely and second most likely class, the more robust the resulting smoothed classifier.
Formally, we write \(G(x) := \text{arg max}_c \, \mathcal{P}_{\epsilon \sim \mathbb{N}(0, \sigma_{\epsilon}^2 I)}(F(x + \epsilon) = c)\) for the smoothed classifier. This smoothed classifier is guaranteed to be robust, i.e., predict $G(x + \delta) = c_A$, under all perturbations $\delta$ satisfying $\lVert \delta \rVert_2 < R$ with $R := \sigma_{\epsilon}\Phi^{-1}(\underline{p_A})$, where $c_A$ is the majority class, $\underline{p_A}$ the lower bound to its success probability $\mathcal{P}_{\epsilon}(F(x + \epsilon) = c_A) \geq \underline{p_A}$ and $\Phi^{-1}$ the inverse Gaussian CDF. As $\underline{p_A}$ increases, so does $R$.
Ensembles
Instead of a single model $f$, we now consider a soft ensemble of $k$ models $\{ f^l \}_{l=1}^k$:
\[\bar{f}(x) = \frac{1}{k} \sum_{l=1}^{k} f^l(x)\]We obtain different models $f^l$ by varying only the random seed for training.
Variance Reduction via Ensembles for Randomized Smoothing
Now, we will show theoretically why ensembles are particularly suitable base models. As shown in the illustration below, ensembling reduces the prediction’s variance over the noise introduced in RS, leading to a larger certification radius $R$.
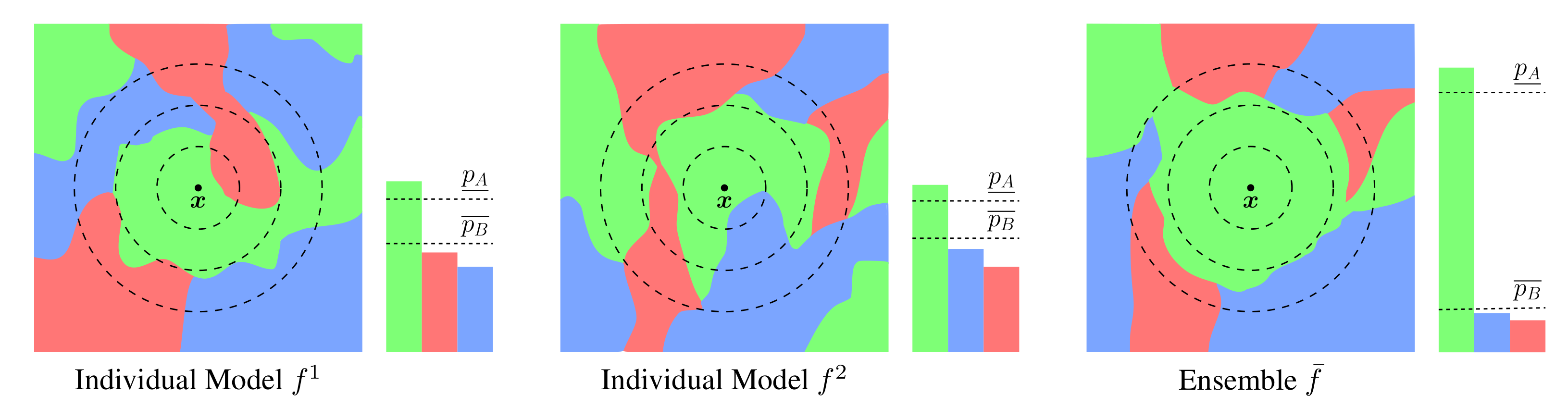
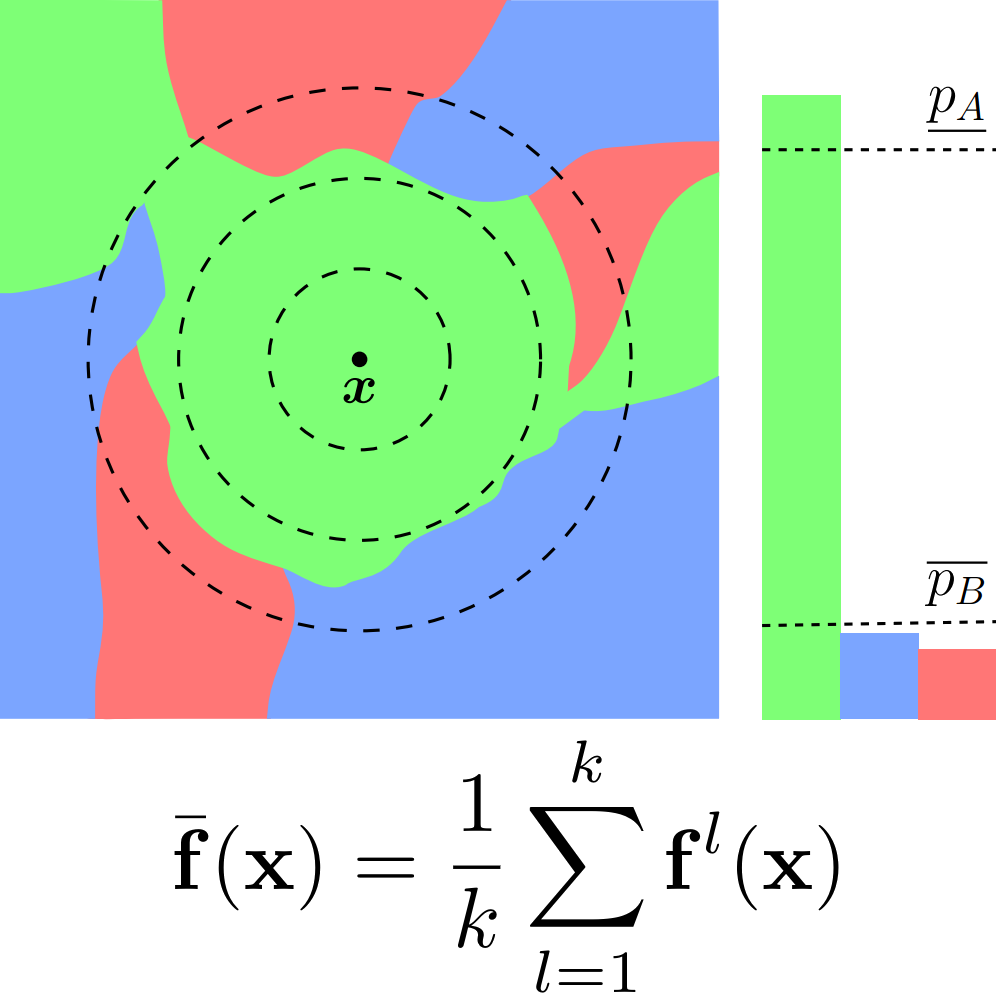
Illustration of the prediction landscape of base models $f$ where colors represent classes. The bars show the class probabilities of the corresponding smoothed classifiers. The individual models (left, middle) predict the same class for $x$ as their ensemble (right). However, the ensemble’s lower bound on the majority class’ probability $\underline{p_A}$ is increased, leading to improved robustness through RS.
Formally, we can introduce a random variable $z_i$ for the logit difference between class $c_A$ and the other classes $c_i$. We denote it as `classification margin’ and can compute its variance depending on the number $k$ of ensembled classifiers ($\sigma^2(k)$) and normalize it with that of a single classifier ($\sigma^2(1)$):
\[\frac{\sigma^2(k)}{\sigma^2(1)} = \frac{1 + \zeta_{} (k-1)}{k} \xrightarrow {k \to \infty} \zeta.\]Here, $\zeta$ is a small constant describing the degree of correlation between the ensembled classifiers. We observe that for weakly correlated classifiers, the variance is significantly reduced. Using Chebychev’s inequality, we can translate this reduction in variance into an increase in the lower bound to the success probability of the majority class $c_A$:
\[\underline{p_{A}} \geq 1 - \sum_{i \neq A} \frac{\sigma_i(k)^2}{\bar{z}_i^{\,2}}% = 1\]We see that the success probability goes towards 1 quadratically as the variance is reduced. Assuming Gaussian distributions and estimating all its parameters from real ResNet20, we obtain the following distribution over the classification margin to the runner-up class $c_i$:
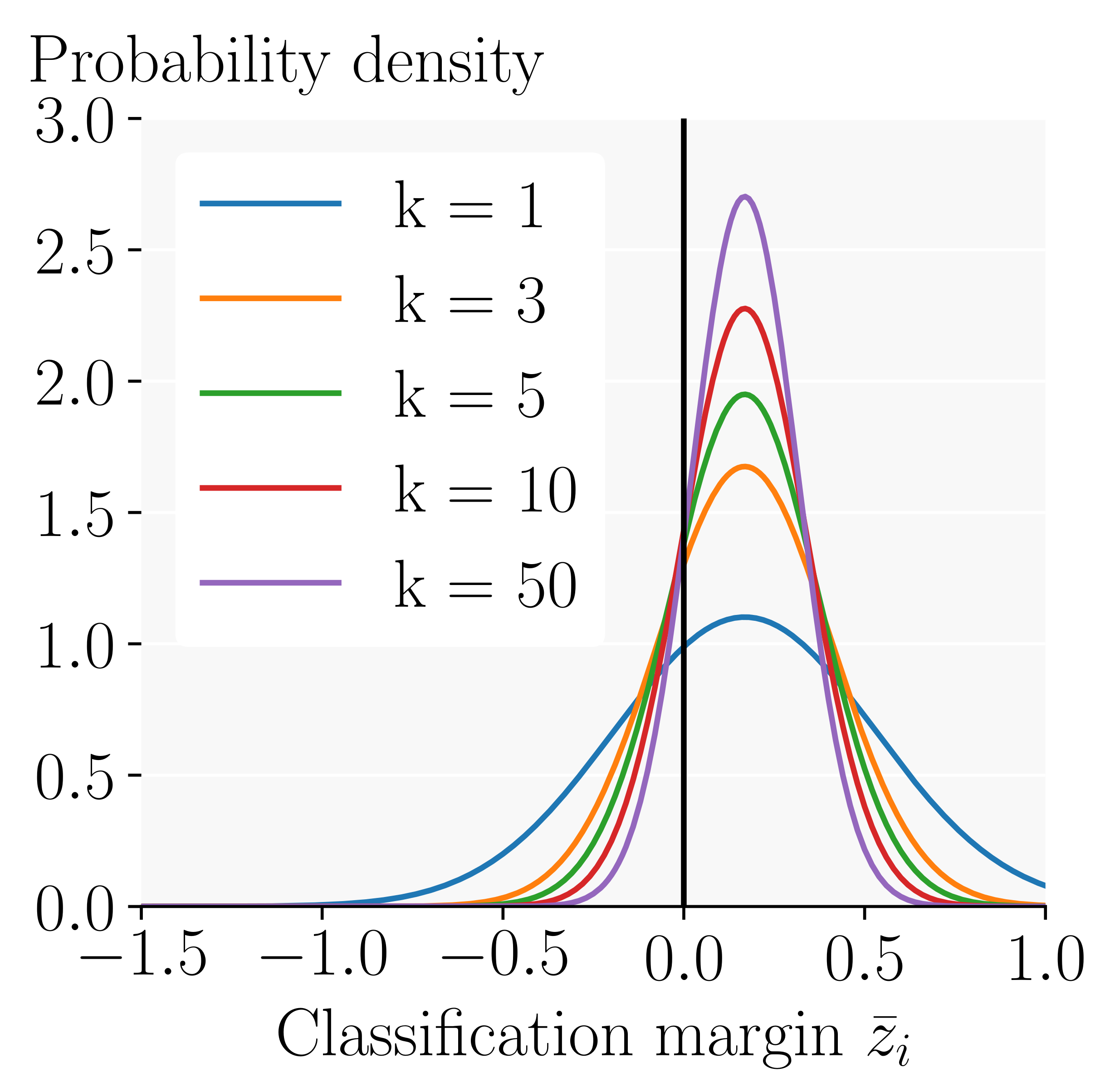
Here, the success probability $p_A$ of the model corresponds directly to the portion of the area under the curve (the probability mass) to the right of the black line. While we see that the mean classification margin remains unchanged, this portion and thus the success probability increase significantly as we ensemble more models.
Certified Radius Having computed the success probability as a function of the number $k$ of ensembled models, we can now derive the probability distribution over the $\ell_2$-radius we can certify using RS.
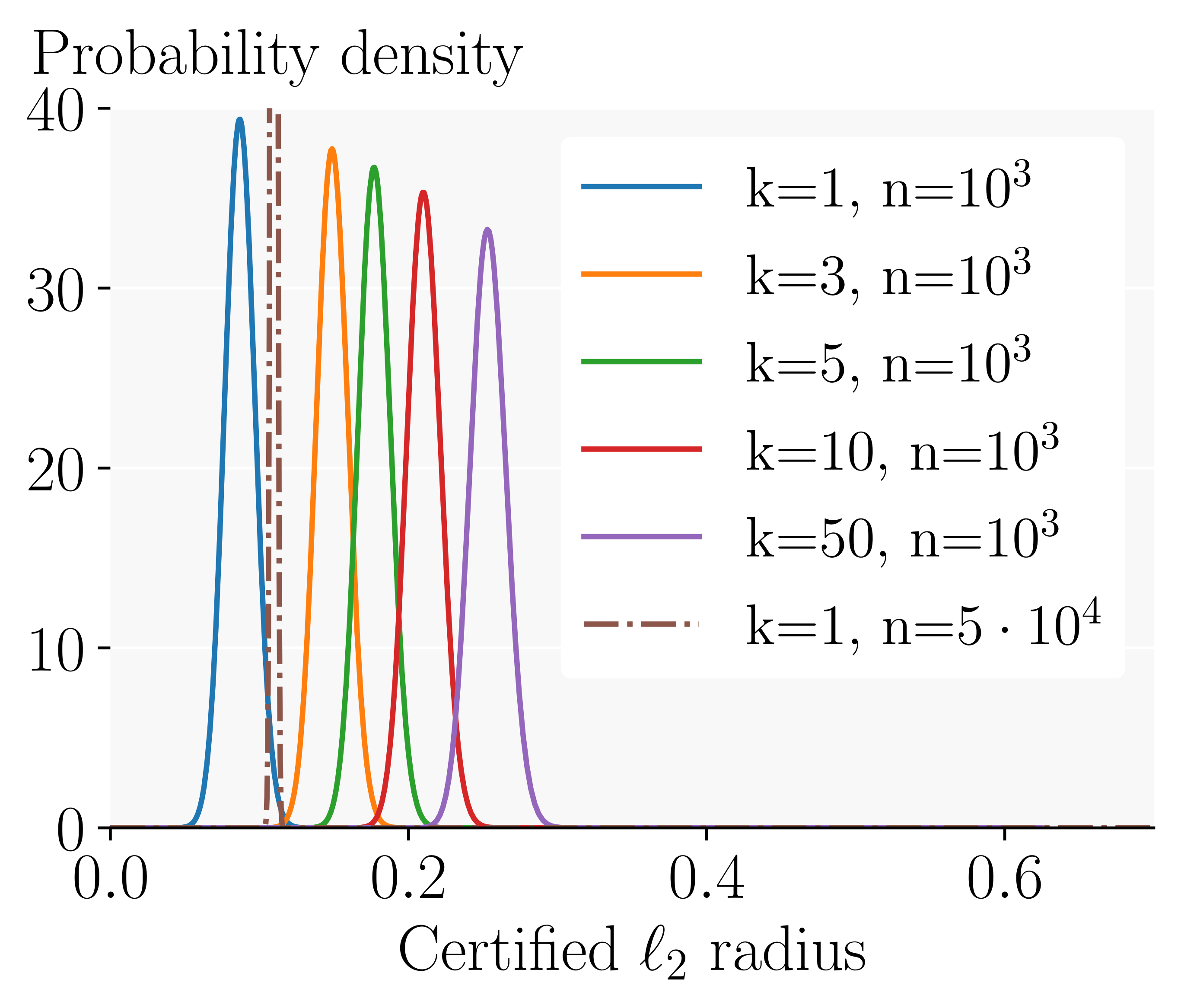
As we increase the number of models we ensemble, the whole distribution shifts to larger radii. In contrast, simply increasing the number of samples used for the Monte Carlo estimation mostly concentrates the distribution and yields a much smaller increase in certified radius.
For a deeper dive and a full explanation and validation of all our assumptions, please check out our ICLR’22 Spotlight paper.
Experimental Evaluation
We conduct experiments on ImageNet and CIFAR-10 using a wide range of training methods, network architectures, and noise magnitudes and consistently observe that ensembles outperform their best constituting models.
CIFAR-10
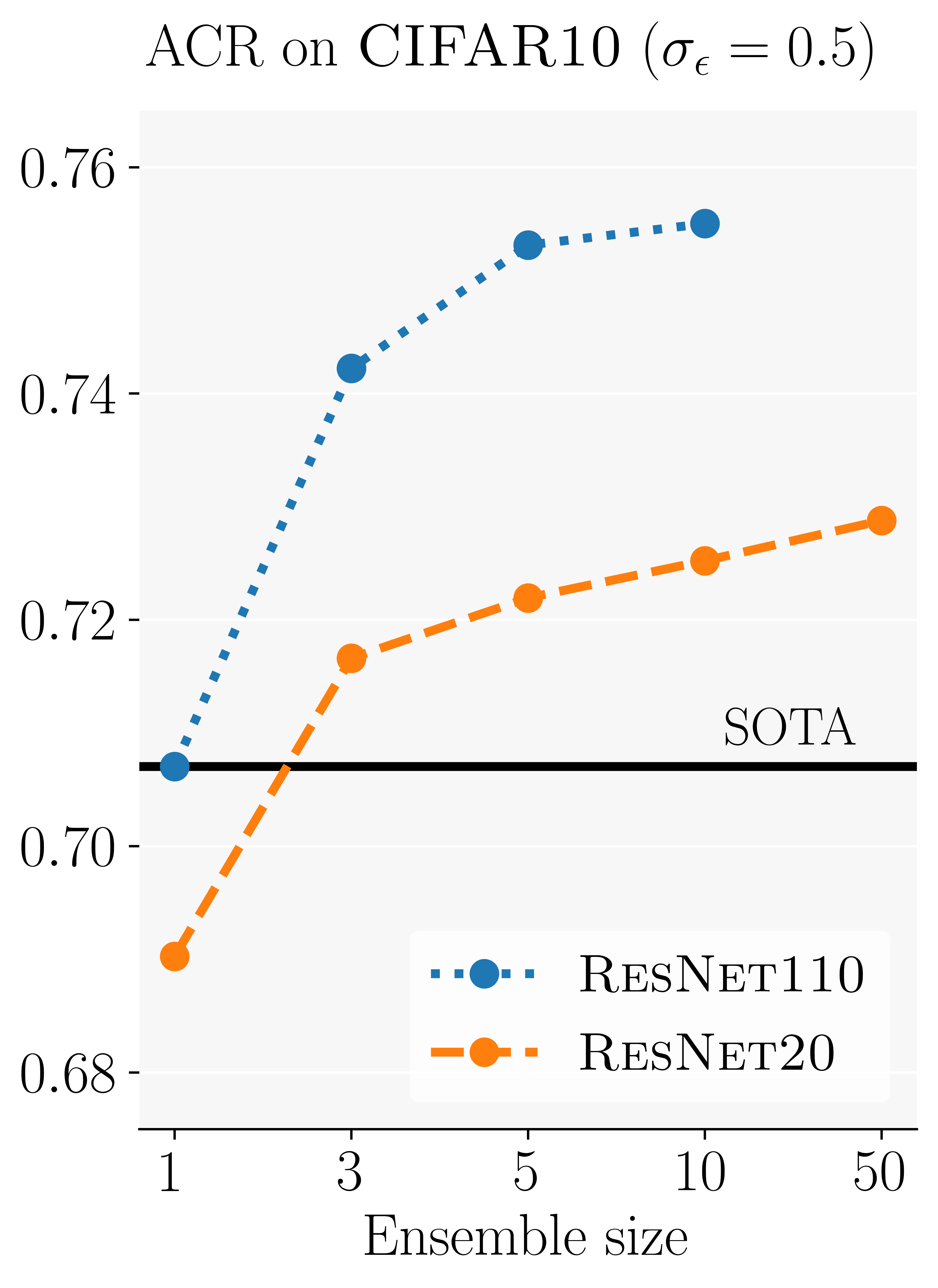
Using an ensemble of up to ten ResNet110’s clearly outperforms the best constituting model (currently SOTA). Even an ensemble of just three ResNet20’s outperform a single ResNet110, despite requiring significantly less compute for training and inference.
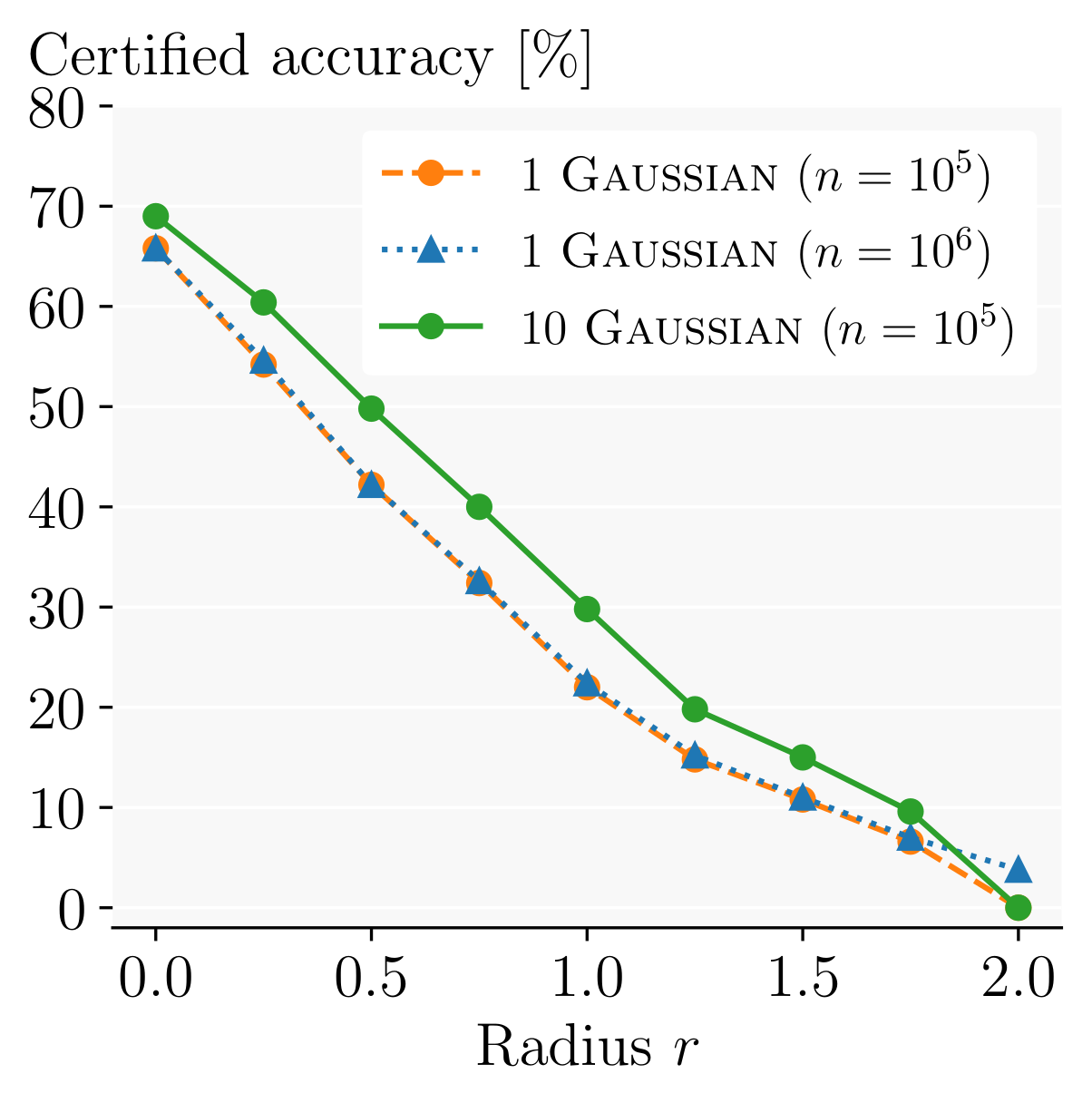
Using more samples with just a single network barely improves the certified radius at all, unless mathematically necessary to achieve a sufficiently high confidence level. Note that this is only the case for very large radii (here 2.0), and, in contrast to our method, does not actually make the model more robust.
ImageNet
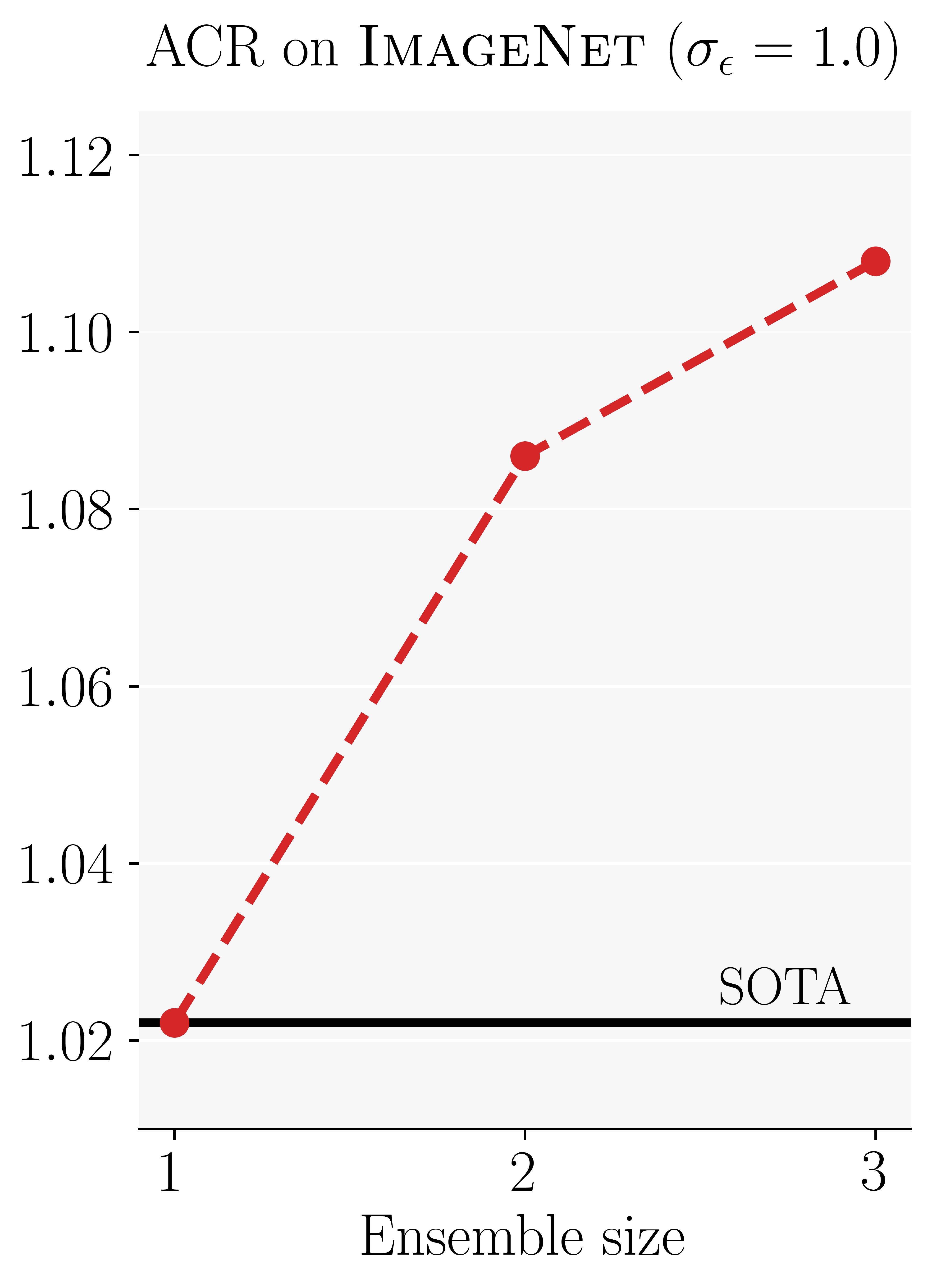
On ImageNet, an ensemble of just three ResNet50’s improves over the current state-of-the-art by more than 10%.
Summary
We propose a theoretically motivated and statistically sound approach to construct low variance base classifiers for Randomized Smoothing by ensembling. We show theoretically and empirically why this approach significantly increases certified accuracy yielding state-of-the-art results. If you are interested in more details please check out our ICLR 2022 paper.

